 Nel fortunato bestseller "La solitudine dei numeri primi" di Paolo Giordano, si legge a un certo punto questa digressione di carattere matematico (forse l'unica dell'intero romanzo):
Nel fortunato bestseller "La solitudine dei numeri primi" di Paolo Giordano, si legge a un certo punto questa digressione di carattere matematico (forse l'unica dell'intero romanzo):I numeri primi sono divisibili soltanto per 1 e per sè stessi. Se ne stanno al loro posto nell’infinita serie dei numeri naturali, schiacciati come tutti fra due, ma un passo in là rispetto agli altri. Sono numeri sospettosi e solitari e per questo Mattia li trovava meravigliosi. Certe volte pensava che in quella sequenza ci fossero finiti per sbaglio, che vi fossero rimasti intrappolati come perline infilate in una collana. Altre volte, invece, sospettava che anche a loro sarebbe piaciuto essere come tutti, solo dei numeri qualunque, ma che per qualche motivo non ne fossero capaci.In un corso del primo anno Mattia aveva studiato che tra i numeri primi ce ne sono alcuni ancora più speciali. I matematici li chiamano primi gemelli: sono coppie di numeri primi che se ne stanno vicini,anzi,quasi vicini, perchè fra di loro vi è sempre un numero pari che gli impedisce di toccarsi per davvero. Numeri come l’11 e il 13, come il 17 e il 19, il 41 e il 43. Se si ha la pazienza di andare avanti a contare, si scopre che queste coppie via via si diradano. ci si imbatte in numeri primi sempre più isolati, smarriti in quello spazio silenzioso e cadenzato fatto solo di cifre e si avverte il presentimento angosciante che le coppie incontrate fino a lì fossero un fatto accidentale, che il vero destino sia quello di rimanere soli. Poi, proprio quando ci si sta per arrendere, quando non si ha più voglia di contare, ecco che ci si imbatte in altri due gemelli, avvinghiati stretti l’uno all’altro. Tra i matematici è convinzione comune che per quanto si possa andare avanti, ve ne saranno sempre altri due, anche se nessuno può dire dove, finchè non li si scopre.
Giordano parla dei numeri primi gemelli, cioè di quelle coppie di numeri primi che differiscono solo di 2.
I due protagonisti del romanzo vengono associati a una coppia di numeri primi gemelli: la rarità di questi speciali numeri diventa così una suggestiva metafora per rappresentare la peculiarità dei due personaggi, e soprattutto l'ineluttabilità del loro avvicinarsi senza mai incontrarsi veramente.
Nel brano che ho riportato, l'autore pone l'accento su due proprietà di queste coppie di numeri.
La prima proprietà è accertata, e corrisponde al fatto che le coppie di numeri primi gemelli tendono a diventare sempre più rari a mano a mano che i numeri crescono.
Sulla seconda proprietà, invece, non abbiamo certezza, e per questo viene chiamata "congettura dei numeri primi gemelli": si tratta dell'ipotesi secondo la quale esistono infinite coppie di numeri primi gemelli.
La prima caratteristica, e cioè la "rarità" dei primi gemelli, trova una rappresentazione matematica in un affascinante risultato trovato nel 1919 dal matematico norvegese Viggo Brun.
Brun considerò le successive coppie di numeri primi gemelli, e calcolò la somma dei reciproci di questi numeri:
 Quanto pensate valga questo numero B? Se invece di limitarci ai soli primi gemelli considerassimo tutti i numeri primi (ad esempio introducendo nella somma anche il reciproco di 23, che è primo ma non è gemello di nessun altro primo), otterremmo una somma infinita. I numeri primi, infatti, sono relativamente rari, e si diradano a mano a mano che i numeri diventano grandi, eppure sono ancora abbastanza numerosi da rendere infinita la somma dei reciproci.
Quanto pensate valga questo numero B? Se invece di limitarci ai soli primi gemelli considerassimo tutti i numeri primi (ad esempio introducendo nella somma anche il reciproco di 23, che è primo ma non è gemello di nessun altro primo), otterremmo una somma infinita. I numeri primi, infatti, sono relativamente rari, e si diradano a mano a mano che i numeri diventano grandi, eppure sono ancora abbastanza numerosi da rendere infinita la somma dei reciproci.Invece, se restringiamo la cosa ai primi gemelli, si ottiene un numero finito, e per giunta anche molto piccolo: la cosiddetta costante di Brun, pari a circa 1,90216.
Il fatto che questa somma sia finita (o, come dicono i matematici, che la serie converga) è una dimostrazione della estrema rarità dei numeri primi gemelli.
Se B fosse risultato infinito (cioè se la serie divergesse), avremmo avuto una prova definitiva della prima proprietà descritta da Giordano, cioè il fatto che esistono infinite coppie di numeri primi gemelli: infatti se i numeri coinvolti nella somma fossero in quantità finita, la somma stessa non potrebbe avere un valore infinito.
Ma la scoperta di Brun prova che così non è, e ad oggi nessuno sa se la sequenza di primi gemelli a un certo punto si arresta o se, al contrario, continua all'infinito.
Come si calcola la costante di Brun? Bè, ovviamente prendendo un certo numero di coppie di primi gemelli e calcolando la somma dei loro reciproci. Il problema è che occorre considerare molte coppie per ottenere un'approssimazione accurata della costante: non deve sorprendere, quindi, che in molte università e centri di ricerca sono a tutt'oggi attivi molti cacciatori di numeri primi gemelli molto grandi, e che vengono calcolate approssimazioni sempre più precise della costante di Brun.
Per eseguire questo tipo di calcoli vengono impiegati sofisticati algoritmi euristici, e la migliore approssimazione ad oggi nota è quella ottenuta nel 2002 da Pascal Sebah e Patrick Demichel, che si presero la briga di considerare tutti i primi gemelli fino a 1016 e produssero l'approssimazione 1,902160583104.
Qualcuno di voi pensa di poter fare di meglio?

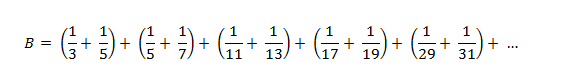










Nessun commento:
Posta un commento
Nota. Solo i membri di questo blog possono postare un commento.