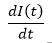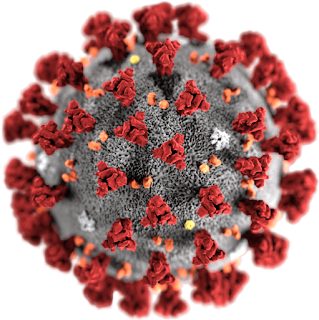
La matematica delle epidemie (parte seconda)

Nicolas Poussin, "La peste di Azoth" (1631), Louvre.

Nella prima parte di questo post abbiamo fatto la conoscenza dei modelli SIR per lo studio delle epidemie.
L'idea di fondo è molto semplice: la popolazione viene suddivisa tra suscettibili (S), cioè individui sani che potrebbero contrarre la malattia, infettivi (I) che si sono ammalati e sono quindi veicolo della malattia, e "recovered" (R), cioè individui che sono "usciti di scena" perché guariti oppure deceduti o ancora messi in isolamento.
I due scienziati Kermack-McKendrick scoprirono che, sotto alcune ipotesi semplificative, gli individui possono passare soltanto dalla classe S alla classe I oppure dalla classe I alla classe R.
La sfida è capire come avvengano questi passaggi, cioè come possano variare nel tempo le numerosità delle tre classi epidemiologiche: in altre parole descrivere l'andamento delle funzioni S(t), I(t) ed R(t). Per riuscire nell'intento, dobbiamo pagare un piccolo prezzo: introdurre un po' di matematica nella nostra discussione.
Ma non temete: se mi seguite con un pizzico di pazienza arriverete sani e salvi alla fine. Con qualche utile nozione in più, almeno spero (intendiamoci, io non sono un epidemiologo o un virologo e nemmeno un medico, ma semplicemente un insegnante e un divulgatore matematico: l'obiettivo di questo post non è sostenere una o l'altra tesi in un campo nel quale non ho alcuna voce in capitolo, ma mostrare come anche in questo ambito è stata usata la matematica per formalizzare alcuni concetti).

Innanzitutto dobbiamo analizzare meglio i meccanismi alla base dei passaggi di classe che ho citato prima. Per esempio, cosa significa che un individuo passa da S a I? Be', semplice: il malcapitato si è infettato ed è diventato contagioso. Perché ciò avvenga, serve un incontro tra un infettivo e un suscettibile: il primo, essendo contagioso, trasmette la malattia al secondo.
La domanda che assilla ciascuno di noi in questi giorni di preoccupazione per il COVID-19 è: quanto è probabile che io contragga il virus? Il calcolo combinatorio e la teoria della probabilità possono darci una mano in questa stima. Supponiamo che N sia il numero totale di individui della popolazione: questo numero è costante perché, come abbiamo visto, Kermack e McKendrick trascurano le nascite e i morti per cause diverse dall'epidemia.
È facile dimostrare che, in una popolazione di N persone, il numero di incontri possibili tra due soggetti è pari a

Per esempio, se ci fossero in tutto N=5 individui (chiamiamoli Alberto, Beatrice, Carlo, Daniele ed Elena), il numero totale di possibili incontri sarebbe

(precisamente: Alberto-Beatrice, Alberto-Carlo, Alberto-Daniele, Alberto-Elena, Beatrice-Carlo, Beatrice-Daniele, Beatrice-Elena, Carlo-Daniele, Carlo-Elena e Daniele-Elena).

Ma quanti di questi possibili incontri è a rischio? Basta che si tratti di un contatto tra un suscettibile e un infettivo: in questo caso è possibile (non certo) che il suscettibile venga contagiato. Il numero di incontri di questo tipo è dato dal prodotto tra il numero degli individui suscettibili S₀ e il numero degli infettivi I₀, ovvero da

La probabilità che un incontro qualsiasi sia a rischio di contagio è quindi uguale al rapporto tra il numero di incontri pericolosi e il numero totale di incontri, cioè al rapporto

Per esempio, se dei nostri N=5 individui, I₀=2 sono già infettivi (poniamo Beatrice e Daniele) e gli altri S₀=3 sono suscettibili, gli incontri a rischio sono S₀I₀=6 (Alberto-Beatrice, Alberto-Daniele, Beatrice-Carlo, Beatrice-Elena, Carlo-Daniele e Daniele-Elena) e la probabilità che uno di questi abbia luogo risulta essere uguale a

L'eremita dei tarocchi

In questa pagina potete trovare un divertente esercizio relativo alle probabilità di contagio in un contesto immaginario di epidemia in un'isola popolata da eremiti... provate a divertirvi a calcolare le probabilità prima di leggere nella pagina i calcoli già svolti!

Se si verifica un incontro a rischio, non è detto che l'infettivo contagi il suscettibile: potrebbe accadere, certo, ma la persona ancora sana potrebbe avere fortuna e salutare l'infettivo senza aver preso il virus. Ovviamente dipende dalla contagiosità della malattia: indichiamo allora con α la probabilità che un incontro a rischio determini un contagio. Preso a caso un incontro tra due individui, la probabilità che questo risulti in una nuova infezione è uguale a

Ammettiamo, per semplicità, che ogni giorno, mediamente, ogni individuo ne incontri un altro: il numero medio giornaliero di nuove infezioni si ottiene allora moltiplicando l'espressione precedente per N:

Se ora definiamo

scopriamo che ogni giorno si verificano

nuovi contagi: questa è anche la quantità di cui ogni giorno diminuisce il numero dei suscettibili.

Abbiamo così determinato che se S(t) è il numero di individui suscettibili in un certo giorno t, il giorno successivo tale numero sarà diventato

Ricordate? Oltre all'evento del contagio, cioè al passaggio tra suscettibile e infettivo, dobbiamo considerare anche una seconda evenienza: il passaggio da infettivo a "recovered", che può corrispondere a una guarigione, ma anche a un decesso oppure alla messa in isolamento di un individuo.
Indichiamo con γ la percentuale di infettivi che ogni giorno passano nella terza classe epidemiologica per uno qualsiasi di questi tre eventi: allora, detto R(t) il numero di individui "recovered" in un certo giorno t, il giorno successivo tale numero sarà cresciuto secondo la relazione

E il numero di infettivi? Be', esso da una parte cresce in virtù dei contagi, ma dall'altra diminuisce per effetto di guarigioni, decessi e isolamenti. Il saldo totale è il seguente:

Queste tre equazioni costituiscono il modello SIR di Kermack e McKendrick in un'ipotesi discreta (perché abbiamo descritto il tutto in uno scenario che avviene "a scatti", anzi a giorni).

Se traduciamo questo sistema in forma continua, si ottiene facilmente questo bel sistema di equazioni differenziali:

Le strane "frazioni" poste nei primi membri di queste equazioni sono le derivate delle tre funzioni S(t), I(t) e R(t) rispetto al tempo, cioè le misure di quanto velocemente queste quantità variano al trascorrere del tempo.
Com'è facile intuire, tutto dipende dal gioco dialettico di quei due parametri β e γ: il primo ci fornisce un indice della contagiosità dell'agente patogeno, il secondo un indice della possibilità che un malato "esca di scena" in quanto guarito, deceduto o isolato.

Le tre classi epidemiologiche del modello SIR e i parametri che regolano il passaggio da una all'altra

In particolare, la seconda equazione del sistema ci dice che la variazione del numero di infettivi

è determinata da un termine "positivo" proporzionale al prodotto S(t)I(t) secondo la costante di proporzionalità β e da un termine "negativo" proporzionale a I(t) secondo la costante di proporzionalità γ. Come si vede facilmente, questa variazione è positiva (cioè gli infettivi aumentano) se

cioè se il rapporto γ/β è minore del numero di suscettibili S(t).
Questo rapporto ha quindi il significato di soglia all'inizio dell'epidemia: se il numero di individui suscettibili è maggiore di questa soglia, l'epidemia può innescarsi e tenderà, in una prima fase, a espandersi in modo molto rapido; se invece è minore, l'epidemia non riesce nemmeno a partire perché il numero degli infettivi si estingue subito.

La buona notizia è che il numero di suscettibili, come abbiamo visto, diminuisce sempre: questo ci assicura che, anche nelle epidemie più devastanti, prima o poi esso scenderà al di sotto del rapporto γ/β, dando avvio alla fase discendente dell'epidemia. In alcuni casi, purtroppo, ciò avviene al prezzo di un elevato numero di vittime.

Concentriamoci ora sul caso "brutto", quello di vera epidemia: S(t) > γ/β.
Moltiplicando entrambi i membri di questa disequazione per β/γ si ottiene una relazione del tutto equivalente:

Quindi se l'inverso del rapporto di soglia moltiplicato per il numero di suscettibili è maggiore di uno, l'epidemia si innesca, altrimenti no. All'inizio dell'infezione, il numero di suscettibili è uguale a N, perché ancora nessuno si è contagiato. Se potessimo fotografare la situazione in quel momento e quantificare il numero

potremmo farci un'idea di come evolverà la situazione: l'epidemia si scatena solo se questo numero è maggiore di 1, altrimenti la diffusione della malattia si arresta sul nascere.

Di questo numero R₀ si è parlato moltissimo in questi giorni su giornali, tv e social: è noto tra gli epidemiologi come "tasso netto di riproduzione" di un'infezione e indica il numero di persone che, in media, un singolo individuo infetto può contagiare durante il proprio periodo infettivo (nell'ipotesi che tutta la popolazione sia ancora suscettibile).

Guardate la tabella qui a fianco. Il morbillo, per esempio, un tasso netto di riproduzione altissimo, che può arrivare addirittura a 18 persone contagiate in media da un singolo malato. Altre malattie risultano meno contagiose, e per il virus che ci sta angosciando in queste settimane è stato per ora stimato un R₀ molto basso, non superiore a 2,5.

Alla luce di queste considerazioni si possono comprendere meglio le misure messe in atto dalle autorità sanitarie e dalle istituzioni per contenere l'infezione. L'obiettivo è, in ogni caso, cercare di ridurre il valore di R₀, oppure, il che è la stessa cosa, cercare abbassare S(t) al di sotto del rapporto di soglia γ/β. Se si raggiunge questo risultato, l'epidemia viene sconfitta. Per farlo, si può agire in diverse direzioni:
1. abbassare il numero S(t) dei suscettibili per sottrarre potenziale terreno di conquista al virus, per esempio sviluppando un vaccino ed effettuando vaccinazioni di massa (ecco perché sono così intensi gli sforzi attuali verso la ricerca di un vaccino contro il nuovo Coronavirus);
2. aumentare il rapporto di soglia γ/β, cosa che si può fare in due soli modi:
  a) alzando γ (risultato conseguibile migliorando le terapie e innalzando così la percentuale di guarigioni);
  b) abbassando β, che rappresenta la facilità del contagio (risultato conseguibile mediante una migliore educazione igienico-sanitaria e soprattutto riducendo le occasioni di incontro tra le persone - esattamente quello a cui mirano le misure adottate in questi giorni, come la chiusura delle scuole, la sospensione degli eventi, e così' via).

Due andamenti possibili per un'infezione

C'è un'ultima considerazione da fare. Alla fine della fiera, l'obiettivo del modello di Kermack e McKendrick è studiare l'andamento della funzione I(t), cioè la curva del numero di individui infettati.
Nella figura a fianco sono mostrati due diversi andamenti possibili per la funzione I(t): ciascuno di essi potrebbe rappresentare la soluzione del sistema di equazioni di Kermack e McKendrick in due diversi casi di infezione.
Chiaramente, l'andamento che presenta il picco corrisponde a un'epidemia in piena regola, molto preoccupante e potenzialmente devastante. Viceversa, l'altra curva, che non fa nemmeno in tempo a salire perché mostra fin dall'inizio una flessione indica un'infezione che passa inosservata perché si esaurisce subito. I modelli SIR ci permettono di distinguere tra queste diverse dinamiche.

Ma c'è una cosa che i modelli SIR non ci possono dire, ed è il numero di vittime che l'infezione può provocare. Se ci avete fatto caso, il modello di Kermack e McKendrick non fa differenza tra individui guariti, deceduti e messi in isolamento: ai fini dell'approccio SIR, in tutti questi casi si verifica una rimozione, nel senso che l'individuo in questione non è più infettivo, e questo basta e avanza per determinare l'andamento della funzione I(t).

Se vogliamo prevedere il numero di decessi, occorre "smembrare" quel parametro γ corrispondente alla percentuale di infettivi che ogni giorno passano nella classe R. Il parametro γ, infatti, è la somma di tre diversi parametri associati ai tre diversi eventi di rimozione: guarigioni, certo, ma anche decessi e quarantene.
Lo specifico parametro legato ai decessi è noto come tasso di letalità dell'infezione: esso è quindi definito come il rapporto tra il numero dei decessi e il numero totale di individui infettivi. Nel corso di un'epidemia, questo indice può variare molto, perché possono modificarsi le condizioni al contorno che rendono la malattia più o meno mortale.
Nella tabella a fianco, possiamo vedere il tasso di letalità stimato per alcune malattie: per alcune è davvero altissimo (evidente il caso dell'Ebola), per altre ovviamente quasi trascurabile (si pensi all'influenza stagionale), mentre il tasso di letalità del nuovo Coronavirus è per adesso stimato attorno al 2%.

Termina qui il breve viaggio di Mr. Palomar nella matematica delle epidemie. Spero che possa giovare per restituire un po' di razionalità e serenità a questi nostri giorni di ansia. Soprattutto, la lezione incoraggiante che possiamo imparare dai modelli SIR è l'inevitabilità dello spegnersi dell'epidemia (ci si augura non ad alto prezzo di decessi): la curva degli infettivi, insomma, prima o poi deve per forza piegarsi verso il basso fino a smorzarsi del tutto.
Come ebbe a dire il grande scrittore portoghese José Saramago nel suo capolavoro Cecità:

Un commentatore televisivo ebbe l’ingegnosità di trovare la metafora giusta quando paragonò l'epidemia, o quel che fosse, a una freccia scagliata verso l’alto, che, nel raggiungere il culmine dell’ascensione, si mantiene per un momento come sospesa, e poi comincia a descrivere l’obbligatoria curva discendente che, a Dio piacendo, e con questa invocazione il commentatore ritornava alla trivialità degli scambi umani e all'epidemia propriamente detta, poi ci penserà la gravità ad accelerare fino alla scomparsa del terribile incubo che ci tormenta (...)

La matematica delle epidemie (parte prima)

Un'immagine del virus SARS-CoV-2,
responsabile del COVID-19

In questi giorni non si parla d'altro.
L'emergenza Coronavirus (COVID-19) ha rapidamente attirato l'attenzione di tutti: sui social e sugli altri media si discute quasi unicamente dell'epidemia e le nostre vite quotidiane sono state fortemente influenzate dalle misure preventive messe in atto dalle autorità.
Anche se non siamo stati tutti direttamente contagiati dal virus, tutti ne parliamo di continuo, tutti ci documentiamo sulle notizie degli ultimi contagi e tutti siamo, almeno in parte, preoccupati dall'evoluzione futura dell'epidemia. Insomma, oltre al virus vero e proprio, ne esiste un secondo, parallelo e "virtuale", legato alla rapida e capillare diffusione delle notizie e alla conseguente apprensione.

Questo fatto ci riporta a una interessante analogia: la dinamica della trasmissione di un virus nella popolazione durante un'epidemia è spesso molto simile a quella che governa la diffusione di un contenuto molto popolare sulla rete, per esempio un meme, un tweet, un video su Youtube, un post su Instagram o su Facebook, e così via. E non è un caso se a questo tipo di contenuti di successo si associa un aggettivo come "virale", che ha origine proprio nel contesto epidemiologico.
Diventa allora interessante comprendere quali siano i meccanismi comuni che regolano questi due ordini di fenomeni: e in questo compito la matematica appare come strumento fondamentale.
Gli studiosi hanno infatti sviluppato alcuni modelli matematici utili per descrivere e prevedere l'andamento della diffusione di alcune epidemie.
Come vengono creati questi modelli? Soprattutto attraverso un'analisi statistica: elaborando dati raccolti su larga scala e relativi all'evoluzione di un contagio, si formulano ipotesi sui meccanismi sottostanti, che poi vengono confermati, perfezionati o modificati da successive osservazioni. In particolare, un buon modello deve saper riprodurre con buona approssimazione la sequenza temporale dei casi di malattia in una comunità di individui.

Daniel Bernoulli

Uno dei primi a tentare un'impresa del genere fu il matematico francese Daniel Bernoulli (1700-1782), che si cimentò nella descrizione quantitativa della diffusione del vaiolo. Verso la metà del Settecento, questa malattia rappresentava un'emergenza straordinariamente grave: era la più grave malattia endemica in quasi tutto il mondo, in Europa era la prima causa di morte, con 400.000 decessi all'anno, e in Francia aveva mietuto numerose vittime anche nella famiglia reale di Luigi XIV (il Re Sole).
Nel suo trattato "Nuova analisi della mortalità causata dal vaiolo e studio dei vantaggi connessi alla vaccinazione preventiva" (1760), Bernoulli propose un modello matematico fondato sulla crescita esponenziale del numero di contagiati, e sulla base di esso dimostrò che l'arma della vaccinazione sarebbe stata molto vantaggiosa per combattere la malattia.
Lo studio di Bernoulli fu molto lungimirante, essendo stato pubblicato quasi quarant'anni prima dell'introduzione del vaccino di Edward Jenner contro il vaiolo.

Attualmente il paradigma di riferimento per la descrizione matematica delle epidemie è il modello proposto nel 1927 dagli scienziati scozzesi William O. Kermack (1898-1970) e Anderson G. McKendrick (1876-1943).
Nel loro articolo "A contribution to the mathematical theory of epidemics", i due ricercatori osservarono che per comprendere la dinamica di un contagio è conveniente suddividere la popolazione in tre classi epidemiologiche:
1. gli individui suscettibili ("susceptible", indicati quindi con S), che non sono stati ancora contagiati ma potrebbero diventarlo;
2. gli individui infettivi ("infectious", I), che sono stati infettati e sono contagiosi;
3. gli individui guariti ("recovered", R), che sono stati infettati ma non sono più contagiosi perché sono guariti (oppure sono morti, o sono stati isolati).

W. Kermack e A.McKendrick

Kermack e McKendrick si accorsero che, nella maggior parte delle epidemie, una persona poteva passare soltanto dalla classe 1 alla classe 2 oppure dalla classe 2 alla classe 3, non essendo possibile un ritorno dalla classe 3 alla classe 2 (ipotizzando che chi è guarito dalla malattia si sia immunizzato).
Il modello specifico pubblicato dai due scienziati si basava su un sistema di equazioni differenziali che permettevano di prevedere l'andamento nel tempo della numerosità delle tre classi epidemiologiche sopra descritte: S(t), I(t) e R(t).
Non è casuale che il modello di Kermack e McKendrick sia arrivato poco dopo quello, molto famoso, proposto da Alfred Lotka e Vito Volterra, che descriveva, sempre attraverso un sistema di equazioni differenziali, la dinamica di un ecosistema in cui interagiscono due specie animali: un predatore e la sua preda.

Più in generale, un modello matematico di epidemia che, ispirandosi all'idea di Kermack e McKendrick, si basa sulle tre classi epidemiologiche S, I e R, viene detto modello SIR. Naturalmente esistono anche tipologie diverse di modelli: per esempio, se la malattia non prevede l'immunizzazione dopo la guarigione (come accade con il raffreddore), la classe R non ha motivo di esistere, e si parla allora di modelli SI.
Il principale obiettivo di un modello SIR è quello di prevedere l'evoluzione di un'epidemia e stimare la porzione di popolazione che contrarrà la malattia. I modelli SIR sono applicabili se sussistono alcune ipotesi:
a) durante l’epidemia la popolazione non si riproduce, cioè non vi sono nuove nascite;
b) durante l’epidemia la causa principale di morte è la malattia epidemica stessa;
c) la popolazione è isolata, cioè non vi sono entrate o uscite rispetto all'esterno;
d) la malattia non ha un periodo di incubazione;
e) dopo la guarigione si acquisisce immediatamente l'immunità;
f) tutti gli individui infetti sono ugualmente contagiosi, indipendentemente dal tempo trascorso dal contagio.

Come è facile intuire, queste ipotesi sono molto semplificative rispetto alla realtà. Per esempio, nel caso del COVID-19 il periodo di incubazione esiste e dura circa 14 giorni, l'immunità dei guariti non è accertata e ovviamente almeno le ipotesi a) e b) non sono realistiche. D'altra parte, nella formulazione di un modello è normale partire da una descrizione che si concentri sugli elementi fondamentali del fenomeno, trascurando quelli che vengono riconosciuti come dettagli di contorno: un po' come quando nella determinazione delle traiettoria di un proiettile si trascura l'attrito con l'aria, in quanto poco rilevante ai fini del calcolo.
Sulla base delle suddette ipotesi, la dinamica di un modello SIR è abbastanza semplice. All'inizio dell'epidemia, la numerosità della classe dei suscettibili, cioè degli individui non ancora contagiati, diminuirà progressivamente a causa dei contagi, mentre la classe degli infettivi si ingrosserà per la stessa ragione. Al crescere degli infettivi, maggiore sarà la probabilità di un suscettibile di essere contagiato, e quindi l'aumento degli infettivi tenderà inizialmente ad accelerare (non a caso Bernoulli, pur partendo da ipotesi molto diverse, aveva pensato a un andamento esponenziale).
A un certo punto, però, alcuni individui cominceranno a passare dalla classe degli infettivi a quella dei "recovered", perché nel frattempo sono guariti, oppure deceduti, oppure messi in isolamento. Da questo momento in avanti tutto si giocherà sul saldo tra i due passaggi: finché vi saranno più contagi che rimozioni (guarigioni più decessi più isolamenti) l'epidemia resterà nella sua fase ascendente, ma quando cominceranno a prevalere le rimozioni si entrerà nella fase discendente. Un fatto è certo: il numero dei suscettibili è sempre decrescente e il numero dei rimossi è sempre crescente.

Tipico andamento di una epidemia secondo lo schema SIR

Quello sopra è un grafico che mostra un possibile andamento di un'epidemia secondo l'approccio SIR: si nota subito la fase ascendente degli infettivi, che culmina in un picco massimo e che è seguita da una fase discendente; parallelamente, i suscettibili diminuiscono sempre e i guariti aumentano sempre.

Ora, torniamo per un attimo all'analogia con la diffusione di contenuti virali nella rete: si può comprendere subito come l'idea di Kermack e McKendrick sia applicabile anche a questo contesto.
Immaginiamo che oggi qualcuno pubblichi in rete un meme potenzialmente destinato a diventare un fenomeno di internet.

"The dress"

Al momento della pubblicazione, rispetto alla potenzialità "viralità" del meme, tutta la popolazione mondiale appartiene alla classe dei suscettibili, perché nessuno ha ancora visto il meme ma potrebbe farlo in futuro. Man mano che le persone scoprono il meme e la condividono a loro volta, questi passano dalla classe dei suscettibili a quella degli infettivi: diventano infatti "vittime" del contenuto virale, cioè se ne appassionano e sono attive nel diffonderlo verso altre persone. Col passare del tempo, sempre più persone cesseranno di interessarsi al contenuto e smetteranno di diffonderlo, passando così nella classe dei "guariti".

Nel 2015 venne postata sulla piattaforma di microblogging Tumblr l'immagine di un vestito che divenne subito virale a causa di un'illusione ottica che suscitava nel pubblico la domanda: "il vestito è bianco e oro, oppure blu e nero?"

La viralità del fenomeno "The dress"

L'immagine diventò rapidamente virale: nel giro di sole 48 ore il post ottenne 400.000 interazioni; nei giorni immediatamente successivi, molti milioni di persone videro l'immagine e la condivisero attraverso i principali social network.

Il grafico a sinistra mostra, in modo semplificato, come il fenomeno denominato "The Dress" si manifestò nella sua viralità: anche in questo caso si distinguono i tre gruppi S (le persone che non hanno ancora visto l'immagine), I (le persone che l'hanno vista, se ne sono appassionati e la stanno condividendo) e R (le persone che si sono disinteressati definitivamente del vestito).

Le domande che sorgono a questo punto sono molteplici. Quali condizioni devono verificarsi affinché un'infezione possa essere definita epidemica e, come tale, si diffonda secondo uno schema di viralità come quello descritto dai grafici sopra riportati? Quali altri andamenti sono possibili? Quale tipo di dinamica sta mostrando il Coronavirus che sta seminando il panico in questi giorni?
Tutto dipende da alcuni parametri fondamentali, che caratterizzano l'infezione: nella prossima parte di questo post vedremo quali sono e scopriremo quali sono le possibili dinamiche di un modello SIR. Restate in contatto!

Katherine Johnson, la donna che ci portò nello spazio

Katherine Johnson, la matematica statunitense che contribuì in maniera decisiva al successo dei programmi spaziali americani (in particolare le missioni Apollo che nel 1969 portarono l'uomo sulla Luna), è scomparsa oggi all'età di 101 anni.
Afroamericana e originaria della Virginia, grazie alla sua determinazione e al suo straordinario talento matematico riuscì gradualmente a superare le discriminazioni razziali e gli ostacoli segregazionisti che nell'America degli anni '50 e '60 ancora esistevano, fino a imporsi come una delle figure più fulgide e influenti della storia della scienza del secolo scorso.
La sua bellissima storia è raccontata nel film del 2016 "Hidden figures" (nella versione italiana "Il diritto di contare").

Nata il 26 agosto del 1918, Katherine dimostra fin da bambina doti matematiche fuori dal comune. I suoi genitori, comprendendo l'importanza di incoraggiare i suoi studi, la iscrivono al liceo della contea di Kanawha, dato che la contea di Greenbrier, nella quale la famiglia risiede, non sostiene l'istruzione superiore per gli studenti di colore.
A soli 13 anni ottiene il diploma di scuola superiore. Iscritta al college della Virginia Occidentale, Katherine frequenta tutti i corsi di matematica disponibili, ampliando il suo già straordinario bagaglio di conoscenze. Al college trova il sostegno di alcuni professori, come W. W. Schieffelin Claytor, il terzo afroamericano a ottenere un dottorato in matematica, e la scienziata Angie Turner King, che l'aveva seguita già negli anni del liceo.
Si laurea a soli 18 anni, ovviamente a pieni voti. Nonostante le sue capacità eccezionali, Katherine deve purtroppo fare i conti con il suo essere afroamericana in un contesto ancora molto chiuso e razzista, e la migliore opportunità lavorativa che riesce a trovare è un lavoro come insegnante di matematica, francese e musica in una piccola scuola elementare per bambini di colore.

Ma qualcosa, per fortuna, si muove. Nel 1939, in seguito a una sentenza della Corte Suprema del Missouri, la Virginia Occidentale decide di abbattere le barriere razziali che ancora erano in vigore per l'iscrizione alle scuole di specializzazione: Katherine Johnson e altri due studenti maschi sono i primi afroamericani ammessi alla graduate school della West Virginia University.
Katherine lascia l'incarico di insegnamento ed entra nel corso di matematica, ma poco dopo decide di interrompere gli studi e dare la priorità alla famiglia (si è appena sposata con James Goble, con cui avrà tre figli).

Più avanti, Katherine Johnson torna a insegnare; ma è soltanto nel 1952 che viene a sapere da un parente che la NACA ("National Advisory Committee for Aeronautics", l'agenzia che sei anni dopo diventerà la NASA) cerca donne di colore da assumere nella sezione "West Area Computing" della sede di Langley, in Virginia. Katherine si candida e viene selezionata: la sua responsabile, Dorothy Vaughan, la assegna a un progetto della divisione di ricerca sul volo, e ben presto il suo contratto a tempo determinato viene stabilizzato.
Il suo lavoro consiste nell'analizzare i dati raccolti nel corso dei voli di prova degli aerei, ad esempio per investigare le cause di incidenti. Alla fine del 1956 suo marito muore di cancro, lasciandola sola con i tre figli.
Le lavoratrici di colore come lei sono soggette, sul posto di lavoro, a una segregazione rispetto ai loro colleghi bianchi, ma grazie alla sua grande determinazione Katherine riesce a far fronte con serenità a queste barriere razziali e di genere.

Poi, nel 1957, con il lancio del satellite sovietico Sputnik, la storia cambia. E con essa anche la vita di Katherine. Il governo americano decide infatti di spingere fortemente verso la ricerca nel settore spaziale. Katherine Johnson è una risorsa preziosa nel nuovo scenario: conosce la geometria analitica come nessun altro in quegli uffici della NACA, e questo le permette di distinguersi agli occhi dei dirigenti ed emergere al di sopra dei più brillanti colleghi maschi.

Nel 1958, nel suo nuovo ruolo di ingegnere aerospaziale all'interno della neonata NASA, contribuisce allo storico documento "Notes on space technology", un report tecnico che avrebbe costituito una importante base di partenza per i programmi spaziali degli anni successivi.
L'anno dopo, Katherine calcola la traiettoria e la finestra di lancio per il primo volo spaziale con equipaggio, la missione Mercury-Redstone 3 del 1961, assegnata ad Alan Shepard.

Nel 1962, in occasione del volo orbitale di John Glenn con la Mercury Friendship 7, la NASA ricorre per la prima volta a computer elettronici per i calcoli delle traiettorie: ma l'astronauta stesso si rifiuta di volare a meno che Katherine Johnson, ormai considerata un'autorità in materia, non confermi i risultati ottenuti dalle macchine.
Glenn chiede di "chiamare la ragazza" e di farle risolvere le stesse equazioni implementate nei computer, ma a mano, utilizzando al più la calcolatrice di cui dispone sulla sua scrivania.
"Se lei dice che i dati calcolati dal computer vanno bene", afferma Glenn, "allora sono pronto a partire". Il volo di Glenn si rivela un successo e segna un punto di svolta nella competizione spaziale tra USA e URSS.

In seguito Katherine lavora direttamente con computer elettronici, e la stima di cui gode contribuisce a infondere fiducia nelle nuove tecnologie. Nel 1969 calcola la traiettoria per il volo dell'Apollo 11 verso la Luna.

In seguito collabora alla missione Apollo 13, aiutando gli astronauti a ritornare sani e salvi sulla Terra dopo i problemi incontrati nel volo. Lavora infine al programma Space Shuttle e all'Earth Resources Satellite (Landsat).
Nel 1986 termina la sua lunga carriera a Langley.

Nel 2015, all'età di 97 anni, il presidente Obama le conferisce la Medaglia presidenziale della libertà, la più alta onorificenza civile americana. Nel 2017 la NASA le dedica un centro di ricerca in Virginia.

La storia di Katherine Johnson, assieme a quella di Dorothy Vaughan e di un'altra matematica afroamericana che lavorò alla NASA, è stata raccontata nel film del 2016 "Hidden Figures" (nella versione italiana "Il diritto di contare"), diretto da Theodore Melfi e basato sul libro omonimo di Margot Lee Shetterly. Il ruolo della Johnson è stato interpretato dall'attrice Taraji P. Henson.

La pellicola è stata candidata a tre premi Oscar nel 2017. Durante la cerimonia di premiazione, la novantottenne Johnson è stata acclamata dal pubblico con una standing ovation. Nel video qui sotto potete vedere una delle scene del film, relativa al volo orbitale di John Glenn.

   

Il suo contributo alla scienza astronautiche e al successo dei programmi spaziali è enorme. Sono numerose le pubblicazioni scientifiche di cui Katherine Johnson è coautrice. Nel sito della NASA potete trovare un elenco dei suoi articoli più significativi e altri documenti sulla carriera e sulla vita di Katherine Johnson. La sua figura è tanto più significativa se si considera, a fianco del suo contributo scientifico, quello relativo al progresso della società americana.

Oggi, in occasione della sua morte, James Bridenstine, l'amministratore della NASA ha rilasciato questa dichiarazione:

La nostra famiglia della NASA è triste nell'apprendere la notizia che Katherine Johnson è deceduta questa mattina a 101 anni. È stata un'eroina dell'America e la sua eredità come pioniera non sarà mai dimenticata.

Buon viaggio, Katherine.

Numeri coprimi, ritardi e... stomp-stomp-clap!

Ho deciso di scrivere questo post invogliato dall'imminente Carnevale della Matematica di febbraio, come da tradizione ospitato dai magnifici Rudi Mathematici. Il tema scelto è il "ritardo", declinato in tutte le sue possibili accezioni.
Gli amici Rudi ironizzano spesso sul ritardo con cui la loro celebre e-zine mensile tende a uscire: tuttavia, per quanto ne so, mai hanno perso un colpo, il che dimostra che i loro ritardi sono in realtà cosa trascurabile rispetto alla magnificenza della loro ormai più che ventennale opera divulgativa. Se c’è un colpevole e recidivo ritardatario, invece, questo è proprio Mr. Palomar, che spesso e volentieri scompare per mesi dai radar. Per questo, mi è sembrato particolarmente significativo raccogliere il guanto di sfida dei Rudi e proporre una mia variazione sul tema del “ritardo”.
Per declinare questo concetto in chiave matematica, ho deciso di prenderla larga, e di partire dai numeri coprimi. Ma che c’azzecca, chiederete voi. Abbiate pazienza e provate a seguire il mio filo logico (se ne esiste uno...).

Chiudete gli occhi e pensate a due numeri interi e positivi qualsiasi. Fatto? Bene, adesso controllate se questi due numeri hanno almeno un fattore primo in comune, oppure nessuno. Per esempio, se avete scelto il 9 e il 21, c’è un fattore primo comune a entrambi, ed è 3. Questo perché sia 9 che 21 sono divisibili per 3. Se invece avete pensato, poniamo, a 12 e 35, non c’è alcun fattore primo comune. In questo secondo caso si dice che i numeri scelti sono coprimi oppure primi fra loro. Due numeri coprimi non hanno alcun divisore comune a parte il numero 1. Detto altrimenti, due numeri sono coprimi se il loro massimo comune divisore è 1.

Un'interpretazione molto suggestiva del concetto di coppia di numeri coprimi è collegata al piano cartesiano. Immaginate che il piano cartesiano sia disseminato di paletti, posti in maniera regolare in tutti i punti di coordinate intere. Dati due numeri a e b,consideriamo il punto P le cui coordinate sono proprio a e b: se P è "visibile" dall'origine, cioè nessun "paletto" si frappone tra l'origine e il punto stesso, allora a e b sono numeri coprimi. Per esempio, nella Figura 1 si vede che i numeri 9 e 4 sono coprimi.

Figura 1 - L'interpretazione "cartesiana" delle coppie di numeri coprimi

Il concetto di numeri coprimi, come potrebbe far intuire il termine utilizzato, è legato all'idea di numero primo? In parte sì. È facile comprendere che due numeri primi sono sicuramente anche primi fra loro. Comunque, affinché due numeri siano primi fra loro non è necessario che essi siano numeri primi.

Qual è la probabilità che due numeri interi positivi scelti a caso siano coprimi? Non è facilissimo calcolare questa probabilità. Potremmo farci un’idea grossolana utilizzando un approccio statistico, cioè eseguendo una serie di prove. Prepariamo una certa quantità di bigliettini, per esempio cento, sui quali scriviamo i numeri interi compresi tra 1 e 100. Poi estraiamo a caso una coppia di bigliettini e verifichiamo se i due numeri estratti sono coprimi o no. Se ripetiamo l’operazione per un numero abbastanza elevato di volte, ci accorgeremo che le coppie sono coprime circa nel 60% dei casi. In base alla legge dei grandi numeri, questo ci autorizza a ipotizzare che la probabilità cercata sia all'incirca uguale a 60%, cioè a 0,6.
Ma questa è una dimostrazione empirica, non rigorosa dal punto di vista matematico. Proviamo allora a ragionare in modo diverso. Qual è la probabilità che, preso a caso un numero intero positivo, questo sia divisibile per un certo numero primo p? Per esempio, estraendo a caso un numero intero compreso tra 1 e 100, qual è la probabilità che esso sia divisibile per 7? Be’, i numeri divisibili per 7 sono 7, 14, 21, 28, 35, e così via. Uno su sette. Il fatto che stiamo considerando i numeri fino a 100 è irrilevante. La probabilità cercata è quindi, in generale, uguale a 1/p.
E se invece di un solo numero ne estraiamo due, a caso? Qual è la probabilità che entrambi siano divisibili per il numero primo p? Trattandosi dell’intersezione di due eventi indipendenti, essa è uguale al prodotto delle singole probabilità, cioè a

È un po’ come la probabilità di ottenere 2 lanciando due dadi: equivale alla probabilità di ottenere 1 su entrambi i dadi, cioè

 
La probabilità che nessuno dei due numeri estratti a caso sia divisibile per il numero primo p, a
questo punto, è la probabilità dell’evento complementare, cioè è uguale a

È analogo a determinare la probabilità di non ottenere 2 lanciando due dadi: è uguale a

I due numeri scelti a caso sono coprimi se entrambi non sono divisibili per qualsiasi numero primo. Anche in questo caso siamo di fronte all'intersezione di eventi indipendenti: la probabilità che questo avvenga è quindi uguale al prodotto

Figura 2 - Eulero in un
francobollo svizzero

Lo so, probabilmente starete pensando: adesso che abbiamo espresso la nostra agognata probabilità in questo strano modo, cosa ci abbiamo guadagnato? Apparentemente non è facile calcolare il valore di quella produttoria e nemmeno stimare se esso si aggira intorno a 0,6 come ipotizzato mediante le prove empiriche.
Eppure, a chi ha qualche familiarità con l’analisi e con la teoria analitica dei numeri sarà forse venuta in mente la celebre formula del "prodotto di Eulero": 

con x reale maggiore di 1.


Da questa formula deriva che la nostra probabilità è uguale a

cioè all'inverso della funzione zeta calcolata in 2. Ora, dobbiamo dirci fortunati, perché lo stesso Eulero ci viene in soccorso nuovamente, questa volta con la sua famosa soluzione del “problema di Basilea”, risalente al 1735: la zeta di Riemann calcolata in 2 vale esattamente

per cui possiamo esultare: la probabilità che due numeri interi positivi scelti a caso siano coprimi è uguale all'inverso di quel numero, ovvero a

Quanto vale questo numero? Circa 0,608: e questo conferma i risultati delle prove empiriche di cui parlavo prima.
Un'avvertenza per il lettore curioso e desideroso di approfondimento: in un mio post di otto anni fa avevo parlato di questi due risultati di Eulero. In quel post sottolineavo la sorprendente presenza di π in un teorema che nulla ha a che vedere con la geometria, ma che scaturisce da una serie formata dagli inversi dei quadrati dei numeri interi positivi. Anche in questo caso non possiamo trattenere un’esclamazione di meraviglia nel constatare come la celebre costante dei cerchi salti fuori anche in questo calcolo di probabilità relativa a coppie di numeri coprimi.

Benissimo. Vi starete però chiedendo cosa c’entra tutto questo con l’idea di ritardo. Chi ha letto il mio libro “Matematica rock. Storie di musica e numeri dai Beatles ai Led Zeppelin” (Hoepli, 2019) sa che il capitolo 2 è dedicato alla celebre base ritmica di "We Will Rock You" dei Queen (sì, proprio quella: "stomp-stomp-clap! stomp-stomp-clap!") e in particolare a come l’autore Brian May riuscì a rivestirla di un effetto di riverbero basato appunto su numeri coprimi.

Come ben sa chi si occupa di musica, il riverbero si verifica quando un’onda sonora viene riflessa, anche più volte, da superfici poste lungo il proprio cammino: l’ascoltatore percepisce così non soltanto l’onda originaria, ma una miscela formata da questa e dalle onde riflesse.
Per simulare artificialmente un effetto di riverbero, il suono originale viene sovrainciso assieme a sue copie “ritardate” di qualche millisecondo (ms), in modo da imitare l’effetto del rimbalzo su una superficie riflettente (per la verità l’intensità dei suoni ritardati viene anche attenuata, così come nella realtà gli echi sono sempre meno forti del suono originale, avendo perduto parte della loro intensità nel corso del loro cammino).
Più precisamente, il chitarrista dei Queen prese ciascuno degli "stomp" e dei "clap" (registrati dai quattro della band in una chiesa sconsacrata alla periferia di Londra) e lo sovraincise più volte, introducendo ritardi diversi e, una volta misurati in millisecondi, primi fra loro.
Per esempio, come indicato nella Figura 3, potrebbe aver scelto 4 ms, 9 ms e 25 ms.

Figura 3 - Una possibile scelta di ritardi coprimi nel riverbero di "We Will Rock You"

Perché questa singolare scelta? Supponiamo che May non avesse scelto ritardi coprimi: ci sarebbe stato allora almeno un divisore comune ad alcuni di questo ritardi. Per fissare le idee, poniamo che tra i ritardi introdotti sul nostro "stomp", vi sia un divisore comune uguale a 10 ms.
L’onda sonora associata al nostro "stomp" è la somma delle sue armoniche, ciascuna caratterizzata da una frequenza multipla di quella del suono fondamentale (o, in modo equivalente, da un periodo che è divisore del periodo del suono fondamentale): se tra queste armoniche ve n’è una con periodo pari a 10 ms, essa presenterà i propri picchi di massima intensità intervallati da una distanza temporale di 10 ms.
In altri termini, se all'istante zero l’onda presenta un picco nel punto A, essa presenterà nello stesso punto un picco di uguale intensità all'istante 10 ms, all'istante 20 ms, all'istante 30 ms, e così via.

Figura 4 - La copertina di "Matematica rock"

Poiché 10 ms è divisore comune tra i ritardi scelti per il riverbero, in almeno due di questi istanti cominceranno a sommarsi anche alcune ripetizioni del nostro "stomp" perfettamente in fase con l’onda originaria, dando origine a un’onda complessiva più intensa di quella iniziale.
L’effetto finale sarà un’amplificazione selettiva delle componenti armoniche caratterizzate da periodi uguali o multipli rispetto ai ritardi scelti per il riverbero. In modo analogo, altre frequenze risulteranno fortemente attenuate, se non cancellate del tutto, come risultato della somma tra picchi e valli.
Qual è la conseguenza di tutto questo? Un’alterazione sgradevole e poco realistica del suono riverberato. Insomma, qualcosa da evitare assolutamente.
Scegliendo ritardi coprimi, Brian May evitò questo rischio.
Se volete approfondire la questione complessiva della matematica di "We Will Rock You", potete trovare pane per i vostri denti nel mio libro "Matematica rock".
Se la base ritmica del famoso pezzo dei Queen è, ancora oggi dopo più di quarant'anni, così potente, irresistibile e trascinante, un po’ di merito lo dobbiamo riconoscere  alla matematica, in particolare ai numeri coprimi, e anche ai ritardi. Vedete? Il ritardo non viene sempre per nuocere.
Delay will rock you!

Dividere per zero (parte seconda)

George Berkeley

L’impossibilità di assegnare un valore alla divisione per zero è divenuto un solido pilastro della matematica soltanto in tempi molto più recenti: uno dei primi riferimenti è presente nel saggio The Analyst pubblicato nel 1734 da George Berkeley.
D’altra parte, è possibile convincersi di questo anche senza ricorrere a false dimostrazioni come quella precedente. Per esempio, a scuola abbiamo imparato che 6∶3=2 perché 2∙3=6. Analogamente, se, dato un certo numero a diverso da zero, potessimo calcolare il risultato della divisione a∶0, la moltiplicazione di questo per zero dovrebbe restituirci a. Per esempio, se 4∶0 fosse un numero, moltiplicando questo numero per zero dovremmo ottenere 4. Ma lo sanno tutti che moltiplicando un numero qualsiasi per zero si ottiene irrimediabilmente zero. Quindi la divisione per zero è impossibile.
E se lo stesso a fosse uguale a zero? In questo caso il ragionamento da svolgere sarebbe un po’ diverso: il risultato della divisione 0∶0, moltiplicato per zero, dovrebbe restituire zero. Per quanto appena detto, qualsiasi numero potrebbe andare bene, cioè la divisione 0∶0 potrebbe avere un risultato qualsiasi. Ma in matematica non possiamo permetterci il lusso di avere operazioni indeterminate, in cui qualsiasi numero è un risultato accettabile. La divisione tra due numeri deve avere un unico risultato corretto, altrimenti la dobbiamo bollare come priva di significato. Così anche la divisione di zero per se stesso non è definita, è un nonsense matematico.

Non siete ancora persuasi che la divisione per zero rappresenta il crimine matematico più nefando e imperdonabile? Lasciatevi allora convincere da un esempio musicale. Immaginate che una rock band debba registrare dodici canzoni per il prossimo disco e che decida di suddividerle in gruppi, così da programmare al meglio le giornate di lavoro in studio di registrazione. Se i pezzi sono già ben rodati, può darsi che in un giorno si possano produrre tutti e dodici i brani: in tal caso basterà un’unica giornata di lavoro (12∶ 12 = 1). Se invece si decide di registrare 6 canzoni al giorno, serviranno 2 giornate (12∶ 6 = 2). Se la band volesse fare le cose in modo molto puntiglioso, potrebbe decidere di dedicare un’intera giornata a ciascun brano, impiegando così ben 12 giorni per completare il disco (12∶1 = 12). E se i musicisti, presi da un’improvvisa svogliatezza, decidessero di registrare zero brani al giorno? Naturalmente le dodici canzoni non vedrebbero mai la luce, nemmeno dopo un numero infinito di giornate, e addio sogni di gloria. In altri termini, sommando tra di loro tanti zeri otteniamo sempre zero e non possiamo mai arrivare a 12. Quindi la divisione 12∶0 non ha alcun risultato sensato.
Un ragionamento analogo potrebbe essere sviluppato fissando il numero di giornate di lavoro anziché quello di pezzi per sessione. Se la band decide di lavorare per 12 giorni, registrando un numero fisso di pezzi a giornata, dovrà dedicarsi ogni giorno a 1 solo brano (12∶ 12 = 1). Volendo concludere le sessioni dopo 6 giorni, ogni giornata sarà dedicata a 2 canzoni (12∶ 6 = 2). E così via. Se i musicisti volessero cavarsela in una sola giornata, registrerebbero tutti i pezzi in una sessione (12∶ 1 = 12). Ma se pensassero di impiegare zero giornate, saremmo autorizzati a dubitare della loro sanità mentale, perché non c’è modo di programmare le 12 registrazioni se sul calendario non ci sono date riservate a questa attività. Ancora una volta abbiamo constatato che non è possibile dividere 12 per 0.

Torniamo ai Pet Shop Boys e alla loro “Two Divided by Zero”. Come abbiamo visto, Chris Lowe era erroneamente convinto che il risultato della divisione per zero fosse una quantità infinita. Se avesse dato retta a Neil Tennant e a Bobby Orlando, che si ricordavano dell’illegalità di questa operazione aritmetica, all’interpretazione metaforica “due divisi da nulla” avrebbe potuto aggiungere un ulteriore, ingegnoso significato: è assurdo provare a dividere i due amanti protagonisti della storia, così come è impossibile tentare di dividere due per zero.
Mi piace fantasticare che la voce sintetica del computer sia stata una trovata del duo britannico per alludere all’aspetto computazionale della divisione per zero. Chiunque si sia cimentato, anche non in maniera approfondita, nell’arte della programmazione, avrà sperimentato almeno una volta la fastidiosa sensazione di vedere un proprio programma arrestarsi sbandierando il triste messaggio di errore “Division by zero”. Se avete una calcolatrice (al limite anche quella virtuale sul vostro computer), vi basta premere di seguito i tasti [2], [:] e [0] per ottenere un simile messaggio al posto di un normale risultato numerico.
La maggior parte dei processori e dei linguaggi informatici genera un errore quando un programma tenta di dividere per zero. Se ne accorsero, loro malgrado, i membri dell’equipaggio dell’incrociatore USS Yorktown il 21 settembre 1997, quando la nave della Marina americana si fermò all’improvviso durante alcune manovre di addestramento al largo di Cape Charles in Virginia.

L'incrociatore americano USS Yorktown

Che cos’era accaduto? Uno dei tecnici della nave, incaricato di risolvere un problema meccanico riscontrato in una valvola del carburante, aveva pensato di calibrare e resettare il dispositivo da remoto, attraverso un’applicazione informatica collegata al database del sistema di controllo della propulsione. Per eseguire l’intervento, digitò uno zero in uno dei campi dell’applicazione, ma questa tentò di dividere un numero per la quantità nulla inserita dal tecnico, generando uno sciagurato errore di divisione per zero. Come dicono gli informatici, l’applicazione andò in crash e innescò una malaugurata catena di errori che provocò infine il blocco totale della nave. La Yorktown era stata utilizzata con successo dal 1984, anche in operazioni di guerra, senza mai riportare incidenti, ma quel giorno rimase come morta per due ore e 45 minuti. Alla fine i tecnici riuscirono a sbloccare i motori e a ricondurre la nave nel porto di Norfolk. Proprio l’impossibilità matematica della divisione per zero aveva annichilito gli ottantamila cavalli vapore di quel colossale incrociatore.

Può darsi che l’incidente della Yorktown avesse contribuito ad attirare l’attenzione di molti sulla questione aritmetica della divisione del zero: fatto sta che nel 2003 addirittura un intero album musicale fu intitolato a questa operazione proibita. "Division by Zero" è un CD del 2003 del musicista svedese Hux Flux, al secolo Dennis Tapper, noto per le sue produzioni di psychedelic trance e prematuramente scomparso nel 2018. A Tapper la matematica doveva piacere molto, visto che i suoi brani sfoggiano titoli come "Calculus", "Logarithmic", "Finite Automata", "Numerous Numerics", "Equivalent Equations", "Numbers" (quest’ultimo contiene perfino un frammento tratto dal film Pi di Darren Aronofsky, dedicato al pi greco). Lo strano caso dell’incrociatore americano ebbe un’altra curiosa conseguenza: l’ingresso della divisione per zero nell’immaginario ironico dei nerd, nel mondo dei meme di internet e nello slang della rete. Alla fatidica operazione è infatti associato un significato metaforico che ha che fare con un’azione proibita e al tempo stesso irrimediabilmente catastrofica: un po’ come il leggendario pulsante rosso dello Studio Ovale che, una volta premuto, scatenerebbe la guerra mondiale nucleare (senza la possibilità di premere un altro pulsante di annullamento dell’operazione). In questa giocosa simbologia telematica, la divisione per zero è spesso collegata alla frase interrotta “OH SHI-“: la naturale e disperata imprecazione di chi si è accorto di aver compiuto un errore analogo a quello del tecnico della Yorktown… ma troppo tardi.

Un internet meme associato alla divisione per zero

In alcuni sistemi informatici, tuttavia, la divisione per zero non è considerata causa di errore, ma produce un risultato associato a una quantità infinita. Sia chiaro: questo non significa che la questione della divisione per zero sia controversa o soggettiva e che si possa affermare che il risultato dell’operazione sia uguale a infinito.
Insomma, Bhaskara II aveva torto e Tennant ricordava le lezioni di matematica del liceo meglio del collega Lowe. Ma la faccenda non può essere liquidata così: adesso vi devo spiegare cosa c’entra la divisione per zero con il vertiginoso concetto matematico dell’infinito.
Anche se non possiamo eseguire una divisione come 1:0, possiamo tuttavia provare a dividere 1 per numeri via via più piccoli e vedere cosa succede.

Per esempio:

1:1=1
1:0,1=10
1:0,01=100
1:0,001=1000
1:0,0001=10000
1:0,00001=100000
eccetera.

Visto? Man mano che i divisori si rimpiccioliscono, cioè si avvicinano allo zero, i risultati della divisione diventano sempre più grandi. Possiamo esprimere questo fatto affermando che, al tendere del divisore a zero, il quoziente della divisione tende a una quantità positiva e infinita. Attenzione però: questo non significa che possiamo eseguire la divisione per zero. Significa soltanto che la sequenza dei quozienti delle divisioni sopra riportate ha un valore limite: tale valore viene indicato con il simbolo +∞ (“più infinito”). Questo valore non è un numero, ma rappresenta una tendenza, un avvicinamento illimitato a valori positivi sempre più grandi.
Dobbiamo sottolineare un altro fatto. Se, anziché considerare divisori positivi sempre più piccoli e sempre più vicini a zero, avessimo preso in esame divisori negativi sempre più grandi e quindi sempre più prossimi a zero, avremmo ottenuto una sequenza di questo tipo:

1:(-1)=-1
1:(-0,1)=-10
1:(-0,01)=-100
1:(-0,001)=-1000
1:(-0,0001)=-10000
1:(-0,00001)=-100000
eccetera.

In questo caso, al tendere dei divisori a zero, i risultati della divisione diventano numeri il cui valore assoluto è sempre più grande. Tuttavia, trattandosi di numeri negativi, il loro valore limite corrisponde a una quantità infinita ma negativa, indicata con il simbolo -∞ (“meno infinito”).
Il fenomeno è ben illustrato dalla figura seguente.

Valore limite del risultato della divisione per quantità tendenti a zero

Il grafico mostra sull’asse orizzontale i valori di x e sull’asse verticale i corrispondenti quozienti 1:x. Quando x assume valori positivi, anche il quoziente è positivo (infatti il grafico è tutto nel primo quadrante, cioè quello in alto a destra): in particolare, quando ci si sposta da destra verso l’asse verticale perché si considerano valori di x sempre più prossimi a zero, il grafico si impenna verso l’alto, perché i quozienti tendono a inerpicarsi sull’inarrivabile vetta di +∞. Quando invece x è negativo, lo è anche il corrispondente quoziente (e il grafico è contenuto nel terzo quadrante, ovvero quello in basso a sinistra): quando ci si avvicina da sinistra verso l’asse verticale considerando valori di x sempre più vicini a zero, il grafico precipita in basso, per rappresentare la tendenza dei quozienti all’irraggiungibile abisso di -∞.
Una cosa è certa ed evidente anche dalla figura: il grafico non si azzarda mai a toccare l’asse verticale. Vi si avvicina indefinitamente, sia da destra che da sinistra, quando x si avvicina sempre di più a zero, ma si guarda bene dal raggiungerlo, perché x non può mai valere esattamente zero. I matematici usano il termine asintotico (dal greco asymptotos, che significa “che non si incontra”) per indicare un avvicinamento di questo tipo, eterno, costante ma mai coronato dal successo.
A me tutto questo ricorda molto la vicenda di un innamorato che, irresistibilmente attratto dalla persona amata, le si avvicina sempre più, ma per un incantesimo beffardo non riesce mai a raggiungerla: una sorta di tragedia romantica in chiave matematica. È una metafora di segno opposto rispetto a quella concepita da Tennant e Lowe in “Two Divided by Zero”: là, infatti, i due protagonisti sono uniti per l’eternità e non si divideranno mai.
In entrambi i casi a stabilire i destini ultimi dei protagonisti è la divisione per zero, anzi la sua impossibilità. Non osate scherzare con questo fuoco, cari lettori. Non arrischiatevi a scavalcare le recinzioni innalzate dall’assurdità di questa operazione, non sognatevi mai di scrivere uno zero sotto una linea di frazione: non vorrete mica causare un’avaria a qualche incrociatore americano, o provocare un disastro apocalittico come quelli evocati dai nerd della rete, vero?

Dividere per zero (parte prima)

Un giorno del mese di agosto del 1981 due ragazzi si conobbero in un negozio di elettronica sulla Kings Road, nel quartiere londinese di Chelsea, e divennero amici.
Neil Tennant aveva 27 anni: si era laureato in storia sei anni prima, alla North London University, e lavorava come redattore presso case editrici. Chris Lowe era più giovane di cinque anni: era iscritto ad architettura all’università di Liverpool ma quell’estate aveva trovato un impiego a Londra come progettista di scale.
Durante l’adolescenza Tennant aveva imparato a suonare la chitarra e il violoncello, Lowe il pianoforte e il trombone. I due scoprirono subito due grandi passioni comuni: la musica disco e i sintetizzatori. Non passò molto tempo e decisero di fondare una band, con Tennant alla voce e Lowe alle tastiere elettroniche. Il primo nome del gruppo fu West End, dal nome della vasta area di Londra situata a ovest della City e a nord del Tamigi.
Successivamente, ispirati dal negozio di animali che un loro amico gestiva nel distretto di Healing, optarono per Pet Shop Boys. Nel corso dei primi due anni di cooperazione, Tennant e Lowe sfornarono alcune delle canzoni che avrebbero costituito il loro repertorio futuro.

La svolta della loro vita professionale arrivò nel 1983. Tennant ricevette dalla rivista Smash Hits il prestigioso incarico di intervistare i Police a New York. Ma al giovane editor non importava proprio niente di incontrare Sting e compagni: il suo vero obiettivo era atterrare negli States e avvicinare il produttore musicale statunitense Bobby Orlando. Tennant riuscì nel suo intento, e seppe strappare anche la promessa di una collaborazione.
Nel 1984 Orlando produsse il singolo “West End Girls”, che ebbe un certo successo in California, ma passò inosservato altrove. I Pet Shop Boys diedero allora il benservito a Orlando e firmarono un contratto con la Parlophone. Il secondo 45 giri, “Opportunities (Let’s Make Lots of Money)” del 1985, si rivelò un altro fiasco. Ai due non mancava però la tenacia.
Nell’estate del 1985, i Pet Shop Boys ripubblicarono il brano “West End Girls” con il produttore Stephen Hague: e questa volta il successo arrivò, enorme e inaspettato. Il singolo vendette un milione e mezzo di copie e raggiunse la vetta delle classifiche negli Stati Uniti e in molti altri paesi.

La copertina dell'album Please dei Pet Shop Boys

Nel marzo dell’anno successivo uscì il primo album, intitolato Please. Si racconta che fu scelto questo titolo per far sì che i fans potessero entrare nei negozi di musica e chiedere “Can I have the Pet Shop Boys album, Please?”
Please fu il primo episodio di una lunga carriera premiata da una immensa fama planetaria. I Pet Shop Boys hanno venduto 50 milioni di dischi in tutto il mondo e sono considerati il duo musicale inglese di maggior successo della storia.
Come definire il loro stile? Lowe dichiarò di non aver mai amato particolarmente la musica rock e ne è una conferma il titolo del loro brano "How I Learned to Hate Rock and Roll" del 1996. Senza dubbio il synth pop dei Pet Shop Boys è più vicino al filone dance o disco, ma liquidare la loro produzione con queste frettolose etichette sarebbe semplicistico.
Il duo inglese riuscì a forgiare uno stile molto originale, melodico ma impreziosito da arrangiamenti complessi, ballabile ma caratterizzato da testi spesso intellettuali. La rivista musicale americana Billboard li nominò al primo posto tra i gruppi dance di ogni epoca. La produzione di Tennant e Lowe, sempre sorretta da una rara grazia, ha ricevuto apprezzamenti anche dalla critica più esigente.
Oltre a “West End Girls” e “Opportunities”, Please comprendeva  altri pezzi di grande popolarità, come “Love Comes Quickly” e “Suburbia”. La opening track dell’album, invece, è meno nota e fu scritta quando il produttore del gruppo era ancora Orlando. Un giorno Tennant acquistò, come regalo di Natale per il padre, un computer che aveva la capacità di riprodurre ad alta voce formule matematiche. Forse era un modello della Texas Instruments o forse della Sharp.
La voce della macchina, sintetica ma con una venatura malinconica, piacque subito a Neil, ma anche a Chris e a Bobby: i tre pensarono che sarebbe stato bello adoperarla per una canzone, facendo pronunciare al computer la frase “Two Divided by Zero”, ovvero “2 diviso per 0”.

Secondo quanto riportato nel booklet della riedizione 2001 di Please, fu probabilmente Lowe a proporre questa espressione matematica, stimolato dall’idea suggestiva che un numero diviso per zero fosse uguale a infinito. Pare che Neil e Bobby non fossero d’accordo con lui e avessero sostenuto che sui libri di matematica questo tipo di operazione aritmetica viene considerata illegale. Sappiamo che i tre discussero a lungo su chi avesse ragione: tra breve scopriremo anche noi la verità.
Lowe indicò anche una possibile interpretazione metaforica della stessa espressione: “two divided by zero” può essere tradotto anche come “due divisi da nulla”, ovvero “due persone che non possono essere divise da niente al mondo, perché sono una cosa sola”. Questa immagine ne richiamò un’altra: due amanti che corrono via, insieme, verso New York. Nella mente di Tennant si affacciò allora un ricordo della sua adolescenza a Newcastle: lui che di notte andava con gli amici alla stazione, per vedere i treni in partenza per Londra.
Guidato da questa visione romantica poté completare il testo della canzone. Lo stesso Tennant ha raccontato che, dopo aver registrato il pezzo con Bobby Orlando, restituì il computer al padre, ma fu costretto a riprenderselo quando la canzone dovette essere nuovamente registrata con Stephen Hague per l’album Please. Dopo di che di quella macchina si persero le tracce.
Ecco il testo di “Two Divided By Zero”:

Let's not go home, we'll catch the late train
I've got enough money to pay all the way
When the postman calls, he'll deliver the letter
I've explained everything; it's better that way
I think they heard a rumour
(Divided by, divided by) Or someone tipped them off
(Divided by, divided by) It's better to go sooner
(Divided by, divided by) Than call it all off
We'll catch a plane to New York, and a cab going down
Cross the bridges and tunnels, straight into town
Tomorrow morning we'll be miles away
On another continent and another day
Let's not go home
(Divided by, divided by) Or call it a day
(Divided by, divided by) You won't be alone
(Divided by, divided by) Let's run away
Someone spread a rumor
(Divided by, divided by zero, zero)
(Divided by, divided by) Better to go sooner
(Divided by, divided by) Let's run away
So why hang around for the deed to be done
You can give it all up for a place in the sun
When the postman calls we'll be miles away
On a plane to New York and another day
I think they heard a rumour
(Divided by, divided by) Or someone tipped them off
(Divided by, divided by) Better to go sooner
(Divided by, divided by) Than call it all off
Someone spread a rumour
(Divided by, divided by) And someone has to pay
(Divided by, divided by) Let's not go home
(Divided by, divided by) Let's run away
(Divided by, divided by) Let's not go home
(Divided by, divided by) Let's run away

Aveva ragione Chris Lowe a sostenere che due diviso per zero fa infinito? Oppure erano nel giusto i suoi due amici? La questione è vecchia quanto lo è la nozione dello zero. Il primo testo matematico che parla di questo numero e considera accettabile la divisione per zero è il Brahmasphutasiddhanta del matematico indiano Brahmagupta, vissuto nel VII secolo d.C.: ma le definizioni in esso contenute sono confuse e contraddittorie.
Due secoli dopo, un altro indiano, Mahavira, sostenne nel suo trattato Ganita-sara-sangraha che un numero rimane invariato se viene diviso per zero. Infine, uno dei più grandi matematici della storia, Bhaskara II, anche lui indiano ma vissuto nel XII secolo, propose la tesi che sette secoli dopo sarebbe stata appoggiata da Chris Lowe: dividendo un numero per zero si ottiene un numero speciale chiamato infinito. In realtà tutti e tre gli indiani sbagliavano: vediamo subito il perché.

Supponiamo che dividere un numero per zero sia un’operazione lecita, cioè che tale operazione restituisca un risultato numerico. Sotto questa ipotesi l’espressione 1:0 corrisponde a un qualche numero a, anche se non sappiamo di preciso quale. Allora possiamo scrivere:

 0∙(1:0)=0∙a

Sappiamo che moltiplicando un numero qualsiasi per zero si ottiene zero: quindi il risultato dell’espressione precedente è 0.
Adesso viene il bello: con un semplice passaggio algebrico, infatti, l’espressione 0∙(1:0) può essere riscritta come (0:0)∙1. Siccome abbiamo sdoganato la divisione per zero, anche l’espressione 0:0 è consentita e il suo risultato è 1, visto che dividendo e divisore sono uguali: quindi la nostra espressione è complessivamente uguale a 1.
Ohibò! Il risultato è 0 e allo stesso tempo 1! Com’è possibile? Nella nostra dimostrazione ci deve essere per forza un errore. L’unico passaggio logico che può essere messo in discussione è proprio quello in cui avevamo ipotizzato che avesse senso dividere un numero per zero: per dirla con Vasco Rossi, possiamo concludere che questa operazione un senso non ce l’ha (con buona pace di Brahmagupta, Mahavira, Bhaskara II e Chris Lowe).
(continua)

"Il mistero del suono senza numero"

Da molto tempo non postavo recensioni di libri su questo blog. Ho pensato di rimediare a questa mancanza dopo aver letto "Il mistero del suono senza numero", dell'amico Flavio Ubaldini, in arte Dioniso, mente poliedrica capace di spaziare in svariati ambiti (è matematico, informatico, musicista, divulgatore, narratore e drammaturgo). Colpevolmente, mi sono deciso tardi a leggere questo coinvolgente romanzo breve: ma meglio tardi che mai, come si dice, perché la lettura si è rivelata una piacevolissima scoperta.

Il fatto è che non è per nulla facile scrivere narrativa, raccontare storie che sappiano trattenere il lettore, creare tensione, colpi di scena, trame non banali. È ancora più difficile farlo inserendo, nelle storie narrate, concetti di matematica, garantendo il rigore e la precisione e al tempo stesso salvaguardando la piacevolezza della lettura. Ancora più arduo è ambientare la propria storia in un'epoca lontana del passato come quella della Magna Grecia del VI secolo a.C., descrivendo situazioni, luoghi, abitudini realisticamente coerenti con tale periodo.
Ebbene, in questo volume, Flavio Ubaldini è riuscito magistralmente a vincere tutte queste sfide, offrendo al lettore una narrazione convincente e piacevolissima. Non dimenticherete facilmente i protagonisti di questa storia: il divino Pitagora, il ribelle Ippaso, l'affascinante Muia, e poi Filolao, Eratocle e tutti gli altri.

Con una perizia da esperto narratore, Ubaldini tratteggia le loro vicende di amicizia, amore, rivalità e passione intellettuale. Sovrapposti all'avvincente trama del romanzo, emergono alcuni dei più importanti enigmi scientifici che tormentarono gli adepti della scuola pitagorica: la relazione tra numeri e suoni, il teorema di Pitagora sui triangoli rettangoli e le sue possibili generalizzazioni, la scoperta dei numeri irrazionali. Ubaldini li espone con sapiente leggerezza, senza appesantire la storia sottostante.

Consiglio questo libro anche a livello didattico, per percorsi interdisciplinari tra storia, filosofia e matematica.

----------------------------------------------
Flavio Ubaldini
"Il mistero del suono senza numero"
Scienza Express, 2017
144 pagine
ISBN: 978-8896973349