 |
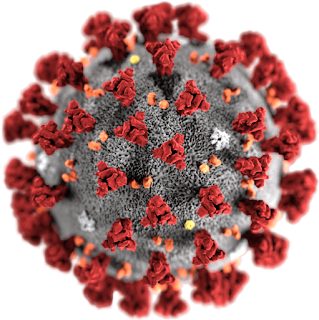
| Un'immagine del virus SARS-CoV-2, responsabile del COVID-19 |
L'emergenza Coronavirus (COVID-19) ha rapidamente attirato l'attenzione di tutti: sui social e sugli altri media si discute quasi unicamente dell'epidemia e le nostre vite quotidiane sono state fortemente influenzate dalle misure preventive messe in atto dalle autorità.
Anche se non siamo stati tutti direttamente contagiati dal virus, tutti ne parliamo di continuo, tutti ci documentiamo sulle notizie degli ultimi contagi e tutti siamo, almeno in parte, preoccupati dall'evoluzione futura dell'epidemia. Insomma, oltre al virus vero e proprio, ne esiste un secondo, parallelo e "virtuale", legato alla rapida e capillare diffusione delle notizie e alla conseguente apprensione.
Questo fatto ci riporta a una interessante analogia: la dinamica della trasmissione di un virus nella popolazione durante un'epidemia è spesso molto simile a quella che governa la diffusione di un contenuto molto popolare sulla rete, per esempio un meme, un tweet, un video su Youtube, un post su Instagram o su Facebook, e così via. E non è un caso se a questo tipo di contenuti di successo si associa un aggettivo come "virale", che ha origine proprio nel contesto epidemiologico.
Diventa allora interessante comprendere quali siano i meccanismi comuni che regolano questi due ordini di fenomeni: e in questo compito la matematica appare come strumento fondamentale.
Gli studiosi hanno infatti sviluppato alcuni modelli matematici utili per descrivere e prevedere l'andamento della diffusione di alcune epidemie.
Come vengono creati questi modelli? Soprattutto attraverso un'analisi statistica: elaborando dati raccolti su larga scala e relativi all'evoluzione di un contagio, si formulano ipotesi sui meccanismi sottostanti, che poi vengono confermati, perfezionati o modificati da successive osservazioni. In particolare, un buon modello deve saper riprodurre con buona approssimazione la sequenza temporale dei casi di malattia in una comunità di individui.
 |
| Daniel Bernoulli |
Nel suo trattato "Nuova analisi della mortalità causata dal vaiolo e studio dei vantaggi connessi alla vaccinazione preventiva" (1760), Bernoulli propose un modello matematico fondato sulla crescita esponenziale del numero di contagiati, e sulla base di esso dimostrò che l'arma della vaccinazione sarebbe stata molto vantaggiosa per combattere la malattia.
Lo studio di Bernoulli fu molto lungimirante, essendo stato pubblicato quasi quarant'anni prima dell'introduzione del vaccino di Edward Jenner contro il vaiolo.
Attualmente il paradigma di riferimento per la descrizione matematica delle epidemie è il modello proposto nel 1927 dagli scienziati scozzesi William O. Kermack (1898-1970) e Anderson G. McKendrick (1876-1943).
Nel loro articolo "A contribution to the mathematical theory of epidemics", i due ricercatori osservarono che per comprendere la dinamica di un contagio è conveniente suddividere la popolazione in tre classi epidemiologiche:
1. gli individui suscettibili ("susceptible", indicati quindi con S), che non sono stati ancora contagiati ma potrebbero diventarlo;
2. gli individui infettivi ("infectious", I), che sono stati infettati e sono contagiosi;
3. gli individui guariti ("recovered", R), che sono stati infettati ma non sono più contagiosi perché sono guariti (oppure sono morti, o sono stati isolati).
 |
| W. Kermack e A.McKendrick |
Il modello specifico pubblicato dai due scienziati si basava su un sistema di equazioni differenziali che permettevano di prevedere l'andamento nel tempo della numerosità delle tre classi epidemiologiche sopra descritte: S(t), I(t) e R(t).
Non è casuale che il modello di Kermack e McKendrick sia arrivato poco dopo quello, molto famoso, proposto da Alfred Lotka e Vito Volterra, che descriveva, sempre attraverso un sistema di equazioni differenziali, la dinamica di un ecosistema in cui interagiscono due specie animali: un predatore e la sua preda.
Più in generale, un modello matematico di epidemia che, ispirandosi all'idea di Kermack e McKendrick, si basa sulle tre classi epidemiologiche S, I e R, viene detto modello SIR. Naturalmente esistono anche tipologie diverse di modelli: per esempio, se la malattia non prevede l'immunizzazione dopo la guarigione (come accade con il raffreddore), la classe R non ha motivo di esistere, e si parla allora di modelli SI.
Il principale obiettivo di un modello SIR è quello di prevedere l'evoluzione di un'epidemia e stimare la porzione di popolazione che contrarrà la malattia. I modelli SIR sono applicabili se sussistono alcune ipotesi:
a) durante l’epidemia la popolazione non si riproduce, cioè non vi sono nuove nascite;
b) durante l’epidemia la causa principale di morte è la malattia epidemica stessa;
c) la popolazione è isolata, cioè non vi sono entrate o uscite rispetto all'esterno;
d) la malattia non ha un periodo di incubazione;
e) dopo la guarigione si acquisisce immediatamente l'immunità;
f) tutti gli individui infetti sono ugualmente contagiosi, indipendentemente dal tempo trascorso dal contagio.
Come è facile intuire, queste ipotesi sono molto semplificative rispetto alla realtà. Per esempio, nel caso del COVID-19 il periodo di incubazione esiste e dura circa 14 giorni, l'immunità dei guariti non è accertata e ovviamente almeno le ipotesi a) e b) non sono realistiche. D'altra parte, nella formulazione di un modello è normale partire da una descrizione che si concentri sugli elementi fondamentali del fenomeno, trascurando quelli che vengono riconosciuti come dettagli di contorno: un po' come quando nella determinazione delle traiettoria di un proiettile si trascura l'attrito con l'aria, in quanto poco rilevante ai fini del calcolo.
Sulla base delle suddette ipotesi, la dinamica di un modello SIR è abbastanza semplice. All'inizio dell'epidemia, la numerosità della classe dei suscettibili, cioè degli individui non ancora contagiati, diminuirà progressivamente a causa dei contagi, mentre la classe degli infettivi si ingrosserà per la stessa ragione. Al crescere degli infettivi, maggiore sarà la probabilità di un suscettibile di essere contagiato, e quindi l'aumento degli infettivi tenderà inizialmente ad accelerare (non a caso Bernoulli, pur partendo da ipotesi molto diverse, aveva pensato a un andamento esponenziale).
A un certo punto, però, alcuni individui cominceranno a passare dalla classe degli infettivi a quella dei "recovered", perché nel frattempo sono guariti, oppure deceduti, oppure messi in isolamento. Da questo momento in avanti tutto si giocherà sul saldo tra i due passaggi: finché vi saranno più contagi che rimozioni (guarigioni più decessi più isolamenti) l'epidemia resterà nella sua fase ascendente, ma quando cominceranno a prevalere le rimozioni si entrerà nella fase discendente. Un fatto è certo: il numero dei suscettibili è sempre decrescente e il numero dei rimossi è sempre crescente.
 |
| Tipico andamento di una epidemia secondo lo schema SIR |
Quello sopra è un grafico che mostra un possibile andamento di un'epidemia secondo l'approccio SIR: si nota subito la fase ascendente degli infettivi, che culmina in un picco massimo e che è seguita da una fase discendente; parallelamente, i suscettibili diminuiscono sempre e i guariti aumentano sempre.
Ora, torniamo per un attimo all'analogia con la diffusione di contenuti virali nella rete: si può comprendere subito come l'idea di Kermack e McKendrick sia applicabile anche a questo contesto.
Immaginiamo che oggi qualcuno pubblichi in rete un meme potenzialmente destinato a diventare un fenomeno di internet.
 |
| "The dress" |
Nel 2015 venne postata sulla piattaforma di microblogging Tumblr l'immagine di un vestito che divenne subito virale a causa di un'illusione ottica che suscitava nel pubblico la domanda: "il vestito è bianco e oro, oppure blu e nero?"
 |
| La viralità del fenomeno "The dress" |
Il grafico a sinistra mostra, in modo semplificato, come il fenomeno denominato "The Dress" si manifestò nella sua viralità: anche in questo caso si distinguono i tre gruppi S (le persone che non hanno ancora visto l'immagine), I (le persone che l'hanno vista, se ne sono appassionati e la stanno condividendo) e R (le persone che si sono disinteressati definitivamente del vestito).
Le domande che sorgono a questo punto sono molteplici. Quali condizioni devono verificarsi affinché un'infezione possa essere definita epidemica e, come tale, si diffonda secondo uno schema di viralità come quello descritto dai grafici sopra riportati? Quali altri andamenti sono possibili? Quale tipo di dinamica sta mostrando il Coronavirus che sta seminando il panico in questi giorni?
Tutto dipende da alcuni parametri fondamentali, che caratterizzano l'infezione: nella prossima parte di questo post vedremo quali sono e scopriremo quali sono le possibili dinamiche di un modello SIR. Restate in contatto!











Aspetto la 2 parte
RispondiEliminaÈ in arrivo tra pochissime ore, domattina alle 7.
RispondiEliminaMolto interessante, anche se ho letto velocemente. Mi ha colpito l'approccio di Bernoulli perchè avevo pensato a qualcosa di simile alla "mappa logistica" che come è noto, descrive l'andamento di una popolazione di insetti. Tale approccio è basato su un'equazione differenziale del tipo Bernoulli-Riccati: http://www.extrabyte.info/2016/03/31/introduzione-alla-mappa-logistica-lequazione-differenziale-di-riccati/ . Precisamente, viene scritta una corrispondente equazione alle differenze finite, dopodiché si passa a un sistema iterato. Questo sistema conosce il famigerato "caos deterministico".
RispondiEliminaNel frattempo mi ero concentrato più sull'aspetto di "propagazione" di un campo virale:
http://www.extrabyte.info/2020/02/27/equazione-di-continuita-bilancio-per-il-coronavirus/
Molto interessante, anche se ho letto velocemente. Mi ha colpito l'approccio di Bernoulli perchè avevo pensato a qualcosa di simile alla "mappa logistica" che come è noto, descrive l'andamento di una popolazione di insetti. Tale approccio è basato su un'equazione differenziale del tipo Bernoulli-Riccati: http://www.extrabyte.info/2016/03/31/introduzione-alla-mappa-logistica-lequazione-differenziale-di-riccati/ . Precisamente, viene scritta una corrispondente equazione alle differenze finite, dopodiché si passa a un sistema iterato. Questo sistema conosce il famigerato "caos deterministico".
RispondiEliminaNel frattempo mi ero concentrato più sull'aspetto di "propagazione" di un campo virale:
http://www.extrabyte.info/2020/02/27/equazione-di-continuita-bilancio-per-il-coronavirus/
Questo commento è stato eliminato dall'autore.
RispondiEliminaChe io sappia, l'approccio di Bernoulli per lo studio del vaiolo si riduceva a una equazione differenziale lineare del primo ordine, con una soluzione di tipo esponenziale. Quindi qualcosa di diverso dall'equazione di Riccati e dalla mappa logistica.
RispondiElimina